This will be an introduction to the slope-intercept form of linear equations. Here we are going to learn about the different kinds of linear equations. Specifically about a different kind of linear equation called two-variable linear equations. Usually, linear equations have just one variable or one unknown factor that is changeable. You are required to find out this common factor. But there are also equations that have two or three variables. Or two or three unknown factors that can change.
In this article, we will learn about the equations that have two variables or two unknown factors that can change. Thus in this article, we will study the slope-intercept form of linear equations that have two unknown factors that can change. We will also study about how to interpret these equations. We will interpret these equations to find the slope of the line. As a result of this, we can also find the Y-intercept of the line whose equation we are interpreting.
Earlier you must have come across the different types of equations. A variable is a factor in an algebraic equation that is unknown and is capable of change. Here we will exclusively talk about equations that have two variables and are called two-variable equations. You must also have heard about the graph of these equations. When we plot these equations on a graph we always get a straight line. In this article, we will talk about how to calculate this y-intercept. We will also talk about how to find the slope. And about how to find out x and y-intercept from the slope-intercept equation

Slope Intercept Form Definition
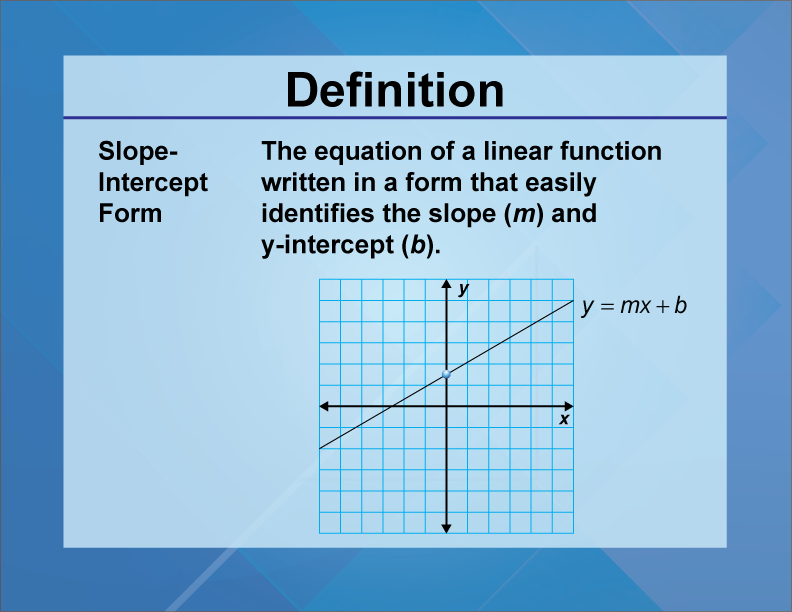
The Slope intercept form is a specific form of the linear equation which is represented in a certain way so that we can find out the slope and y-intercept of a straight line easily from it without having to change the subject of the formula. If the equation was in any other form we would have to rearrange the variables to find out the slope and y-intercept of the straight line.
What are x and y intercepts of a straight line?
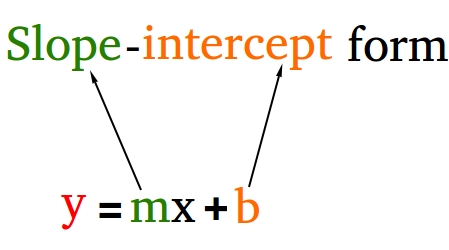
Before delving into the slope-intercept form of the equation of a straight line we must talk about some concepts. These will include the x and y intercepts of a straight line. What are the x and y intercepts of a straight line? Let us assume that there is a line stretching endlessly along the horizontal direction. We will call this line the x-axis. Next, let us assume that there is a vertical line stretching along the vertical direction. We will call this the y axis. The place where the x and y axes cross each other is called the geometrical origin. You must remember that this whole event is taking place in the two-dimensional plane.
Hence any straight line that will ever exist in this two-dimensional plane must cross these two lines I mentioned before. Wherever this straight line crosses the y axis we will obtain a point. The disdain of this point from the origin is called the y-intercept. Similarly, wherever this aforementioned straight line crosses the x-axis we will obtain a point. The distance of this point from the origin is called the x-intercept. The slope of this line is the angle it makes with the x-axis. These preliminary concepts are very important to be able to understand the slope-intercept form.
Representation of the Slope-Intercept Form
Simply, this is how the equation is represented:
y=mx+c
Here y is the y-intercept, m is the slope of the equation, x is the x-intercept and c is the y coordinate of the y-intercept. The two variables in this equation are x and y and the two contents are m and c. In this equation m and c can be any two real numbers. For example, the equation y=6x+7 is in slope-intercept form. So in the equation y=-3x+26. However, the equations 3x+4y=78 and 5x-91y+100 are not in the slope-intercept form. They are in the form we call ax+by+c=0 which is another way of representing linear equations as we spoke about in the earlier portion of the article.
This equation has a lot of practical applications in laboratories. This is because if we find out the equation of a straight line we can substitute the values of x and y alternatively to predict what might happen in similar situations. Thus this equation helps in experimental sciences.
The x and y coefficients of the slope-intercept form of Linear equations
The simplicity of the slope-intercept form of the linear equations comes from the fact that the equation directly tells us the y-intercept and the slope of the straight line! In fact, that is the reason why it is called the slope-intercept form. Here m and c can be any two real numbers. Because it gives the slope and the y coordinate of the y-intercept of the straight line. For example, if the equation of a straight line is y=4x+2 it would mean that 4 is the slope of the line and the y-intercept is 2. Thus the line would cross the y axis at the point (0,2). To calculate the x coefficient we have to make x the subject of the formula and substitute the value of y in the equation.
Word Problems of the Slope intercept form
Question 1: Let us find the straight-line equation that has slope m = 2 and passes through the point (–1, –8).
Solution: Thus, from the slope-intercept form, we know that;
y=mx+c
It is given,
m=2
Thus, from the given information we can find out that;
y = -8 and x = -1
Hence, putting the values in the above equation, we have found;
-8 = 3(-1) + c
-8 = -3+c
c = -8 + 3 = -5
Hence, the required equation will be;
y = 2x-5
Question 2: Let us find the straight-line equation that has slope m = -3 and passes through the point (2, 3).
Solution: Thus, from the slope-intercept form of linear equations, we know that;
y=mx+c
It is given that,
m=-3
From the given information we can also find out that;
y = 3 and x = 2
Hence, after we substitute the values in the given equation, we are able to get;
3 = -1(2) + c
3 = -2 + c
c = 3+2 = 5
Hence, the required equation will be
y = -3x+5
Practice Questions:
- Find the slope of the line y=7x-2
- Calculate the intercept of the line y=x-26
- Find the slope of the line which crosses the line at point (-2,0) and has an intercept of -1
- Calculate the slope of the line y=9x-8
- Find the slope of the line 6y=x-1
FAQs
Frequently asked questions about the slope-intercept form of the linear equation also are:
1)What is the y variable in the slope-intercept form?
The y-intercept in the slope-intercept form equation is the y coordinate where the line crosses the y axis. As we know the slope-intercept equation is y=mx+c. Here y is the y-intercept, m is the slope of the equation, x is the x-intercept and c is the y coordinate of the y-intercept. The two variables in this equation are x and y and the two contents are m and c. In this equation m and c can be any two real numbers.
2) How do you find the y-intercept from the slope-intercept form equation? / What is the constant c in the slope-intercept form equation?
The slope-intercept form equation is y=mx+c. From this equation, we can get the value of the y-intercept which is c. Also, here y is the y-intercept, m is the slope of the equation, x is the x-intercept and c as mentioned, is the y coordinate of the y-intercept. The two variables in this equation are x and y and the two contents are m and c.
3)How do you find the slope from the slope-intercept form equation? / What is the constant m in the slope-intercept form equation?
As we have studied so far, the slope-intercept form of the linear equation is y=mx=c. From this equation, we can find out the slope. The slope is represented by the letter m.
4)How do you find the y-intercept when two points are given?
First, you have to find out any two points on the given straight line. Let us assume that the two points are y1, y2, x1, and x2. From these points also find out the slope m. We can do this by making two linear equations substituting the x and the y in the common equation y=mx+c. After that, simultaneously solve these two equations. The c will get canceled because it will be common in both the equations. After this step is done we will have obtained the value of m which is the slope of the straight line.
Read Also: Tudor Architecture: All you need to know about Tudor Architecture.
The next step will be to find out c or the y coordinate of the y-intercept of the slope-intercept form equation. We can do this by substituting the coordinates of any one of the already given points in the straight line. Substitute the x and the y value from any one of the points already given in the straight line. As a result of this, we will be able to calculate c. Thus by the end of these steps, we will have obtained the values of m and c. Finally, substitute the values of m and c in the mother equation y=mx+c.