Discriminant Know the meaning, definition, formula

So, what does a discriminant mean? One that discriminates. So, all our life, we have heard the term. We might have heard in our social science classes. So, the literal meaning of the word is that it is a distinguishing feature of something. This feature separates it from every other thing. However, that is how the ordinary man would be using the term. But, right now, you are a student of mathematics. And so, you have to apply the term in its mathematical sense. In maths, the discriminant is an idea which we find widely in quadratic, cubic, and such other equations of the higher-order.

When you solve a quadratic or cubic equation, you often find that the teacher has asked you to find the discriminant of the equation. Now, it is just not a question that your teacher is asking simply for the sake of asking. A discriminant has a much more important role to play. It has the ability to analyze the root of the equation. So, with its help, you can come to a conclusion. Therefore, you can understand whether the root is imaginary or real. However, there are various conditions that you need to remember before you can do this. So, in the next few sections, we will see what a discriminant is and how to find it out. Moreover, we will also study why it is necessary or what are its applications in maths.

Discriminant meaning

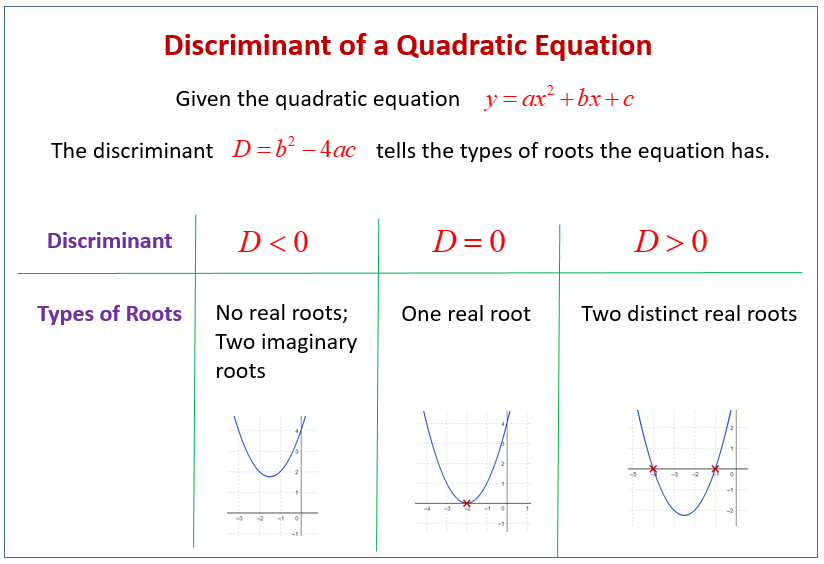
So, at first, imagine a quadratic function. You can imagine something of a higher order as well. However, let us start understanding a discriminant from the very basics. Now, from the equation form, you try finding out the value of the variable, let us say x. So, for this, you have to convert it to the formation that supports Sridharacharyya’s formula. Therefore, the discriminant is the portion of the quadratic formula that lies under the symbol of the square root. So, it is basically b²-4ac. Here, b is the coefficient of x, a is the coefficient of x^2 and c is the constant. However, the importance of this value is huge. So, the discriminant tells us how many solutions the equation can provide. Therefore, there might be one solution. There can be two solutions as well. However, there can be no solution at all.

Two solutions mean there is a “+” or “-” sign before the square root. So, if you add you will get a root. On the other hand, if you subtract the root from b^2, you will get an altogether different value. However, that is not all about it. It might happen that there is no solution as well. This happens when the roots are imaginary. So, there can be a negative square root or something like that. Therefore, this is where the discriminant operates.

Discriminant definition

So, now the question is how do mathematicians define a discriminant. So, a discriminant is a function of the coefficients of a polynomial equation whose value gives information about the roots of the polynomial. Therefore, it finds wide usage in polynomial factoring, number theory, and algebraic geometry. The discriminant is often represented by the delta symbol while doing calculations. However, the term discriminant includes several other generalizations as well. So, it might be the discriminant of a number field in algebra. It can be a discriminant of a quadratic form which is the most popular one. Moreover, it can also be the discriminant of a form, a homogeneous polynomial, or even a projective hypersurface. However, if you look carefully, the three concepts are not much different from each other.

Discriminant of the higher degrees

We generally do not consider the discriminant of a linear polynomial- that is of the first degree. This is because it will definitely be 1. It is so as the conventions for the empty product clearly portray so. Moreover, one of the two blocks of the Sylvester matrix is empty. So, there is no common convention for the discriminant of a constant polynomial. This means the degree of the polynomial is 0. So, as you can well imagine, when the degree is low, finding a discriminant is very simple. However, as the degree becomes higher, the process becomes more complex and difficult. If you want a glimpse of the process, the discriminant of a general quartic has 16 terms. On the other hand, a quintic has one of 59 terms. Moreover, a sextic has as many as 246 terms.

Homogeneity in a discriminant

So, in the coefficients, the discriminant is a homogeneous polynomial. Moreover, it is also so in the roots. Therefore, in that case, it is quasi-homogeneous in the coefficients. So, now consider you have taken a polynomial of degree n. Therefore, the discriminant now will be of degree 2n – n in the coefficients. We can see this in two different ways. Firstly, we will consider the roots and leading term formula. So, here when you multiply all the coefficients with Wilk’s lambda, the roots do not change. However, the leading term gets multiplied with its value.

Secondly, we can take into account how we express it in terms of the determinant. Therefore, the matrix that we will consider is the Sylvester matrix. This is a (2n – 1) x (2n – 1) matrix. So to find its determinant, we have to divide it by an. So, the determinant is homogeneous of degree 2n – 1 in the entries. So, on the division, the degree becomes 2n – 2.

Moreover, the discriminant of a polynomial of degree n must be homogeneous of degree n (n – 1) in the roots.

We should also remember a basic general idea. This is for all the polynomials which are both homogeneous as well as symmetric in their roots. So, we can express them as quasi-homogeneous polynomials in the elementary symmetric functions of the roots.

Discriminant formula

The formula to find the discriminant depends on the equation that you are working with. So, for quadratic equations, you will have a particular formula. For a cubic equation, we will have another one. So, as the degree becomes higher, the formula will also change. This is because if you think when the degree decreases, the number of terms or coefficients also simultaneously increases. This is only natural. There is a generalized formula from which you can find its value from equations of any degree. However, it is complex and difficult to understand. Therefore, let us see the formula for quadratic equations first. We will then go one by one with the cubic and the quadratic. So, we are not going with the generalized one. This is because you generally do not need more than the fourth-degree order in the school.

Discriminant of the quadratic equation

Let us say the quadratic equation is-

ax^2 + bx + c = 0.

Therefore, from here, the value of x = ((-b +/- (b^2 – 4ac)^(½)) / 2a)

However, as we have already seen, x is likely to have two values- once when you add, and once when you subtract.

Now, take out the portion of the root. So, this is b^2 – 4ac. This is the formula for the discriminant of the quadratic function. This is probably the simplest form of discriminant you will ever encounter. However, it is also the one that we most generally use in calculations.

Discriminant of the cubic equation

So now, first we need to consider a cubic equation. Therefore, let us say it is-

ax^3 + bx^2 + cx + d = 0.

So, here in this case, the formula to find out the discriminant is = (b^2 x c^2) – 4a (c^3) – 4d (b^3) – 27 (a^2 x d^2) + 18 ( abcd)

However, there can also be a depressed cubic equation. So, let us say it is in the form of x^3 + px + q = 0.

Therefore, now, the formula to find out the discriminant now will be = – 4p^3 – 27q^2.

Discriminant of the quartic equation

Now, as you can already imagine the equation is going to be quite long. This is because there are four degrees. Similarly, the formula to find out the discriminant will also not be very simple.

Therefore, let us say, the quartic equation is ax^4 + bx^3 + cx^2 + dx + e = 0.

So, now the formula to find out the discriminant is 256 (a^3 x e^3) – 192 (a^2 x b x d x e^2) – 128 ( a^2 x c^2 x e^2) + 144 (a^2 x c x d^2 x e) – 27 (a^2 x d^4) + 144 ( a x b^2 x c x e^2) – 6 ( a x b^2 x d^2 x e) – 80 ( a x b x c^2 x d x e) + 18 ( a x b x c x d^3) + 16 ( a x c^3 x e) – 4 ( a x c^3 x d^2) – 27 (b^4 x e^2) + 18 ( b^3 x c x d x e) – 4 ( b^3 x d^3) – 4 ( b62 x c^3 x e) + ( b^2 x c^2 x d^2)

That indeed is a very complex-looking thing. However, if you start putting the values, it is not as complex as it looks. Moreover, at school, you would hardly come across it. These equations of the higher-order generally function when you are doing some intricate scientific calculations. However, under ordinary circumstances, you generally do not need these at school. So, it is fine!

Discriminant 0

So, a discriminant can be 0 under several circumstances. However, there are a few conditions that we also need to keep in mind. So, a polynomial over a field can have a zero discriminant. However, this can only happen when it has multiple roots in a certain field extension.

So now, coming next, a polynomial over an integral domain can also have a zero discriminant. However, there is a very strict condition that needs to be satisfied. So, in this case, the polynomial along with its derivative must have a non-constant common divisor.

The third case is of a characteristic 0. So, this is the same as telling that the polynomial is not square-free. But, what does not square-free mean? So, it means that the polynomial is divisible by the square of a non-constant polynomial.

The last case is that of a nonzero characteristic p. Therefore, in this case, the discriminant is zero if and only if the polynomial is not square-free. However, being square-free is not the only option here. It might have an irreducible factor as well which you cannot separate. So, what does this mean? Therefore, this means that the irreducible factor is a polynomial in x^p.

Discriminant for real roots

So, discriminant can easily give an idea regarding the nature of roots. Let us consider the case of quadratic equations here. So, if its value is more than zero, then there are 2 roots and both of them are real. On the other hand, if its value is 0, the equation has only one root. However, if its value is less than zero, there are 2 roots and both of them are imaginary.

Discriminant less than 0

So, for a quadratic equation, the discriminant is b^2 – 4ac. Now, if b^2 – 4ac has a value less than zero, then there are two roots of the equation. However, both the roots are imaginary.

Discriminant FAQs

When should you use the discriminant?

So, we mostly use discriminants for quadratic equations. We mostly use them to check if a quadratic equation has two real solutions, one real solution, or two complex solutions.

How many roots are there if there is a discriminant?

By telling if there is a discriminant, what one probably means is having a non-zero discriminant. So, the answer to that is two. However, if it is zero, there is only one root. This means that there is only one real root that repeats itself.