So, if you have taken up science, or subjects like economics and mathematics in high school, calculus has already become a part of your everyday life. Indeed, it helps you do calculations in physics and chemistry which you just cannot do with normal arithmetic or algebra. Therefore, both integration and differentiation become extremely important. However, you cannot learn to integrate if you do not know differentiation very well. This is because you can only join or integrate something when you have already differentiated or broken it down into infinitesimal quantities. So, knowing differentiation with all its rules is very important. It might seem a little overwhelming in the beginning. However, once you get the hang of it, it is really easy. Now, the chain rule is one of the important parts of differentiation. To make it easy, we will see a chain rule calculator and its use here.

So, you can use a chain rule calculator for various reasons. You might want to use a chain rule calculator to make the calculation fast. However, you can also use it to make sure there are no mistakes in the calculation. This is important particularly if you are working with many variables. So, there are high chances that you forget to differentiate one entity at the end because the chain rule involves a complex. Therefore, a chain rule calculator can help you with this process by making a chunk of the calculation easy and swift. Therefore, let us see what a chain rule calculator is and how you can use it for maximum benefit.
Chain rule calculator online
The internet has made everything very easy. So, you need something you can simply click a link and get it done. Therefore, calculus is no exception. A chain rule calculator is therefore a device that gives you the entire derivative of an equation where you can apply the chain rule. So, for an experiment, you can be sure that there are no errors. However, if you have to do it manually, you can always use a chain rule calculator to verify that you are doing it right.
So, on the internet, you will find many a chain rule calculator. Various sites like emath, byju’s, and symbolabs have different derivative calculators. Therefore, a chain rule calculator too falls in them. So, all that you need to do is feed the equation to the calculator. The online chain rule calculator does all the job. In the end, you get to see the resultant derivative. Moreover, most of these calculators do not just give you the answer. So, they also show you the entire process behind it. This is very important. Suppose you are getting a different answer from the calculator’s one. If you check the summing step by step, you will easily identify where you made the mistake. Moreover, this process will help you learn as well. So, it will not feed you a formula that you cannot understand.
Chain rule calculator with steps
So we have already seen there are many chain rule calculators that are available online. However, you might get a little confused regarding how to exactly use them. So, we will show you all the steps that you need to perform or go through.
For this, we are taking the help of an online chain rule calculator available in Symbolabs. Click on “Symbolabs” to find the link that will guide you to the chain rule calculator.
Step 1 to use a chain rule calculator
So, on opening, you will find a box. You will find the words “chain rule” there with d/dx. Therefore, d/dx means a differentiation in respect to x. So, when dx is already given, you have to make sure that the equation that you are feeding to the calculator must be in terms of x. Therefore, what does this mean? Suppose you are doing a differentiation in physics with respect to time, where the variable is t. However, when you are typing the equation in the calculator, make sure you change the “t” to x.
Let us say here, we have the equation- 2( x + 1)2
Step 2 to use a chain rule calculator
So, now you will find a bracket beside d/dx. You must type out the entire equation inside this bracket. If you type anything out of it, the calculator will not differentiate that part. So, you might get a totally different value. Moreover, right on the top, there is a box with every kind of symbol. This makes it very easy to use particularly from a laptop where the keyboard does not have those options. So, you can have an exponent, a square root, or whatever you want.
Read Also: Interval Notation Calculator – An Online Tool to Make Math Easy
So, we should type 2( x + 1)2 within the bracket. Therefore, to type (x + 1) ^2, simply type “x + 1” in a bracket. Then, go to the box containing the symbols. Select the ‘x2” option from there. Therefore, what you have in the box now is d/dx (2 (x + 1)2).
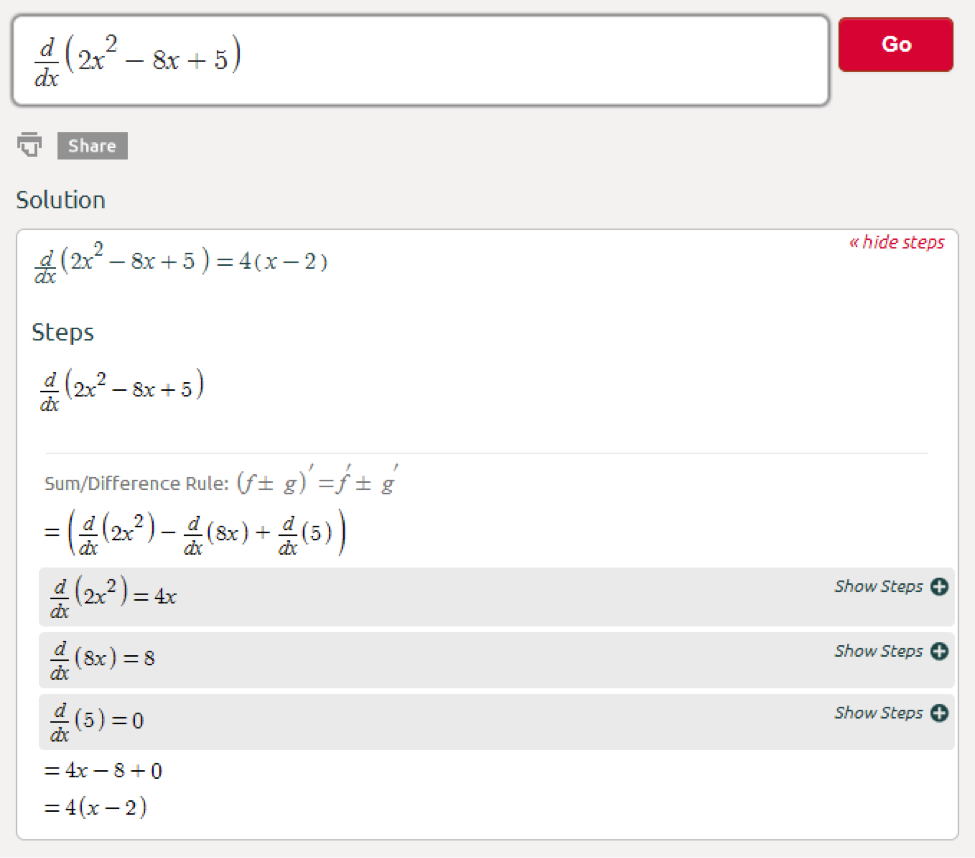
Step 3 to use a chain rule calculator
So, now that you have entered the equation into the chain rule calculator, you have practically completed your job. Therefore, click on the red “go” button. The calculator may take a few seconds to compute.
Step 4 to use a chain rule calculator
So, within a few seconds, you will get the answer. Check the solution box underneath. You will find not only the final derivative but also all the steps leading to the answer. So, in this case, the final answer will be- 4 (x + 1).
However, when you click on the “show steps” button on the solution box, you can see all the steps. Moreover, you can also expand each step and understand them by clicking on the appropriate pop-up.
So, in this case, it will be-
At first, you must take the constant out. So, it will be 2 d/dx( (x + 1) ^2).
Now, the chain rule has to be applied. So, if you do not multiply with the constant what you get is-
2 (x + 1) x d/dx(x + 1), as per the chain rule.
Now, d/dx (x + 1 ) = 1, because d/dx (x) = 1, and d/dx(1) = 0, as it is a constant.
Therefore, the total value that we find after multiplying with the constant is 2 x 2(x + 1) = 4 (x + 1).

Step 5 to use a chain rule calculator
So, as I already said, you can correct your manual calculation too with the help of a chain rule calculator. Suppose, you have got an answer that is different from the calculator’s answer. So, at the end of the solution box, you will find a search engine-like box. On the right of this is a red box that says “verify”. So, you should insert your answer here and the calculator checks it for you! This is particularly important for integration where for the same sum you can have different answers and all of them may be correct. So, it depends on the process that you are following.
However, to avail of this feature, you need to open an account. As soon as you click on the box, there will be two options for opening an account. You can sign up for a free account via Facebook, Google, or your mail ID. However, you can also take a paid subscription for more materials and benefits.
Step 6 to use a chain rule calculator
So, this is the last part. Scroll down and see the plotting of the graph under the graph box. This is very important because this will help you understand what the function is actually like. Moreover, we often face trouble in plotting a function on a graph even after we have calculated it correctly. So, this part solves the problem.

Chain rule calculator calc 3
So, calculus 3 is the part when you deal with multivariate calculus. However, to efficiently do such calculus or understand them, you need to have a strong foundation in single-variable calculus. Therefore, what happens here is that a single equation has more than one variable. So what happens here is that you have to do two intermediate differentiations to get the final value. now let us take a look at our multivariable chain rule and whether a chain rule calculator can at all handle multivariate equations
Chain rule calculator multivariable
So, now let us understand this with the help of an example.
Suppose, your equation is z = xy + y^3. And, you have to find dz/dx. Therefore, y is a different variable. Let us say you have defined y = cos (x^2 + 1).
Now, when you insert this equation into the chain rule calculator, you cannot get the complete result. This is because there is no place where you can tell the chain rule calculator the value of y. So, wherever the variable y was there, the chain rule calculator simply shows dy/dx- as in the differentiation of y with respect to x. However, what you can do now, is again replace the value of y and enter d/dx (cos (x^2 + 1)). So, this gives you the differentiation of y after using the chain rule. Now, you can simply combine them both to get the final answer.
However, the easiest thing to do would have been simply replacing the value of y with cos(x^2 + 1) while entering the mother equation. It would hence have saved a lot of time and labor.
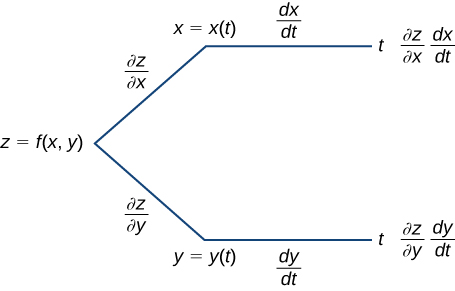
Chain rule calculator 3 variables
So, the process remains the same. You can differentiate thrice with three variables and then combine manually to find the answer. However, that would be an extremely difficult and tedious idea. So, it is better you simply replace all the other variables in terms of x. Therefore, this will make the equation look very complex. Moreover, it will also belong. The answer will be long and complex as well. However, your job will be minimum. So, the chain rule calculator would do everything for you.
Chain rule calculator partial derivatives
So, the concept of partial derivatives comes only when you have more than one variable in the equation. Therefore, when you use partial derivatives, you differentiate the entire equation with respect to one variable. So, all the other variables receive the same state as a constant. Therefore, differentiating them yields a zero. However, your normal chain rule calculator cannot give this result. It is because it will treat the other variables as variables only and not constants. So, for doing this go to the panel on the left-hand side. Now click the partial derivatives option. Now change the dx or dy while inserting the equation with respect to which you want to differentiate. So, the calculator will do your job this way.
How do you solve chain rule problems?
Well, you have a function. However, when you differentiate the function, it still may remain incomplete. So, you again differentiate till you have differentiated the smallest entity. This is a chain process and hence we call it the chain rule. You can find a proper explanation with examples in steps 2, 3, and 4 of the chain rule calculator steps.
How do you combine the product and the chain rule?
So, as we have already seen, you need a product rule when you are multiplying two functions externally. However, it might so happen that one or both of the functions have layered functions inside them. So, in that case, you have to use the chain rule. You can use the chain rule, in the beginning, to simplify each of the composite functions individually. Or you might apply it at once with the product rule when you are handling one or two of the composite functions. The same process applies to if there are more than two functions as well. However, this can be a complex process. So, your chain rule calculator is here to make that easy for you.

Chain rule calculator FAQs
How to use the chain rule calculator?
So, there are roughly three main steps to using a chain rule calculator. Insert the equation properly, click the go button and view the results. However, that is not all about it. Check out the chain rule calculator steps to find a thorough understanding of all the steps that you must follow while using it.

Can you always use the chain rule?
There can be no such rules in calculus, It depends on the equation of what you are handling currently. If your equation is in the product form and has a function within a function, you have to apply it till you reach the smallest function.
Does chain rule work for all functions?
No, the chain rule does not work for all functions. So, you can apply the chain rule only when you have a composite function that has two or more functions inside it. If you have a single function, you cannot use it.
How do you use the chain rule example?
Well, let us take an example. Let us say, y = 5 (x + 3)^2
So, according to the chain rule, h′(x)=f′(g(x))g′(x)
Here, g(x) = (x + 3) and f(g(x)) is (x + 3)^2
Therefore, dy/dx = 5 x d/dx((x +3)^2) x d/dx(x + 3)
= 5 x (2x + 6) x 1
= 5(2x + 6)
How important is the chain rule?
The chain rule is extremely important because if you are not using it, there are high chances you are keeping a composite derivative incomplete. Students make a lot of mistakes here as they forget to use it in long calculations. So, this is why you must use a chain rule calculator.
Is the chain rule the same as the product rule?
No, not at all. The chain rule and the product rule are not the same. They both have very different functions. So, you need to use the chain rule to make sure all the functions are differentiated. On the other hand, you need the product rule to differentiate a product of two or more functions. Therefore, you use a chain rule when there is a function within a function. And, you use the product rule when simply two functions are multiplied from outside.
Does the chain rule apply to partial derivatives?
Yes, the chain rule applies to partial derivatives. In fact, as per the definition, the chain rule for functions of more than one variable involves partial derivatives with respect to all the independent variables. However, if you want a partial derivative, make sure you have clicked the correct option while using a chain rule calculator. This part is very important to avoid getting unwanted results.
Who invented the chain rule?
It was Issac Newton who invented the whole idea of calculus. So, the chain rule is no exception.