First things first, let us have a clear idea of motion itself. Instantaneous velocity might look like a complex thing to deal with. However, once you have a clear idea of the basic things, understanding would not be very difficult. Moreover, try to understand well the derivations of the formula. So, in that way, you can apply it during calculations in an easier way.
So, as well all know motion is a relative thing. Consider you are sitting inside a bus. Now, it passes by a bus stop. Therefore, you are in motion with respect to that bus stop. This is because the bus stop can never move. It is stationary. However, now consider a different situation. So, you are sitting inside a bus. The bus is moving at a constant velocity. However, there is another bus going adjacent to your bus. It is also moving with the same velocity. So, with respect to each other, both the buses are at rest. This is because they are at a parallel velocity. So, now you are looking at someone in the other bus from the window of your bus. However, you will not see them moving. However, both of you are actually moving!
So, from here we get the terms of speed and velocity which define rest and motion. Therefore, as you can well imagine, we cannot discuss instantaneous velocity before we know what velocity is. Moreover, in our everyday lingo, we often interchange the words “speed” and “velocity”. However, in Physics they do not mean the same thing. They represent two different quantities altogether.
What is velocity?
So, velocity is the rate at which a thing is moving in a particular direction. Therefore, mathematically velocity is the ratio of the distance that a moving object covers to the time it takes in covering that distance. However, this alone cannot define velocity unless you are considering the direction. It is important to note this. When you consider the direction of the moving object, you are making a difference from its speed. So, speed is just the rate at which a thing is moving. It does not take into account the direction of the moving object. Therefore while velocity is a vector quantity, speed is a scalar quantity. So again, before we move on to instantaneous velocity, we must know what scalar or vector quantities are.
Scalar and Vector quantities
So, these are terms which we have probably studied in science from quite a young age. For example, the easiest example is that mass is a scalar quantity. However, weight is a vector quantity. This is because mass only considers the amount of matter that is present inside an object. However, for weight, the gravitational force of the earth acting vertically downwards plays a role. So, as you can well understand the most basic difference between scalar and vector quantities is that of direction. While vector quantities have a direction, scalar quantities do not have so.
Definition
So, scientists have defined scalar as a quantity that has a magnitude but no direction. On the other hand, a vector is a quantity that has a magnitude as well as acts in a particular direction.
Instantaneous velocity meaning
So, by now we have understood what velocity is and how it functions. Moreover, we have also seen how it is different from speed. So, now we can discuss what exactly instantaneous velocity is. One can easily understand that the word instantaneous comes from the word instant. So, then, it must be the velocity of a moving object at a particular instant. What does this mean? Therefore, it means that instantaneous velocity is the velocity of an object in motion at a specific point in time. So, you see, it makes so much sense. For instantaneous velocity, unless the object is following an exact straight path, it must change every now and then. This is because in every other case, the direction changes. So, you can already guess that just like velocity, this is also a vector quantity.

Instantaneous velocity definition
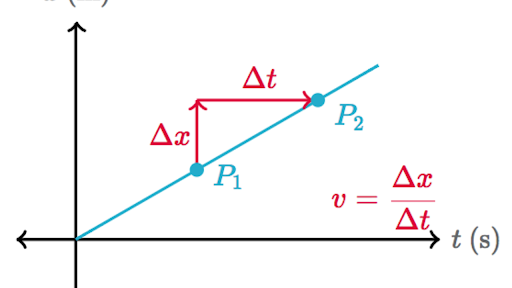
So, we have understood what instantaneous velocity is. Therefore, now, we can take a look at how scientists define quantity mathematically. So, the instantaneous velocity of an object is the limit of the average velocity as the elapsed time approaches zero. That might seem like a lot of confusing words. First, what is average velocity? So, average velocity is the change in distance that an object in motion covers in a particular time period. It must also be in a particular direction. So, average velocity = dv/dt, where d means the change in distance or time.
Read Also: Know about grams to atoms calculator
Now, it is saying that the elapsed time must approach zero. This means that the variable ‘t’ for the time interval approaches zero. So, the time becomes almost null, but not totally null. Now, if you think about it, this is exactly what an instant means. An instant is less than even a second. It might be a fraction of a second but it is not null, because time cannot be zero.

Therefore, since we are handling such minute quantities, we need to find out the value only via calculus. Once you apply calculus, you can consider the limit of the variable “t” to be 0. So, this means, the time approaches 0 but is not 0. Now, consider the distance that the object is covering to be x. Therefore, you can find the final value by simply differentiating x with respect to t when t approaches 0. But, all the while you need to remember it is a vector quantity. So, you need to find out the direction as well if someone asks you to calculate the instantaneous velocity.
Instantaneous velocity formula
So, from the definition, we can well understand how the formula of the quantity will look like. Therefore, it is the derivative of “x” with respect to “t”. So, here x is the distance that the object is covering, and “t” is the time period it takes. Hence, the formula is-
v(t) = (d/ dt) (x (t))
So, v(t) means velocity in a particular time which is the instantaneous velocity. Therefore, in more scientific words, v(t) here means velocity as a function of time. “x (t)”, means the distance that the object has covered in the given time. So, we have to differentiate distance with respect to the time interval. However, the time interval, as we already know, is almost 0 for this case.
Instantaneous velocity and instantaneous speed
So, now we have got an idea of what instantaneous velocity is, both qualitatively and quantitatively. Therefore, the same question again arises. So, what is instantaneous speed? Moreover, how is it different from instantaneous velocity?
Instantaneous speed is nothing more than the magnitude of instantaneous velocity itself. Therefore, the difference between instantaneous velocity and speed is just the same as that of speed and velocity. So, just like speed, instantaneous speed is a scalar quantity. On the other hand, like velocity, instantaneous velocity is a vector quantity. Therefore, this new quantity cannot tell the direction of an object in motion at a particular point in time. But, instantaneous velocity can. So, it is simply the change in distance with respect to the time interval when the time interval approaches 0.
Instantaneous velocity Graph

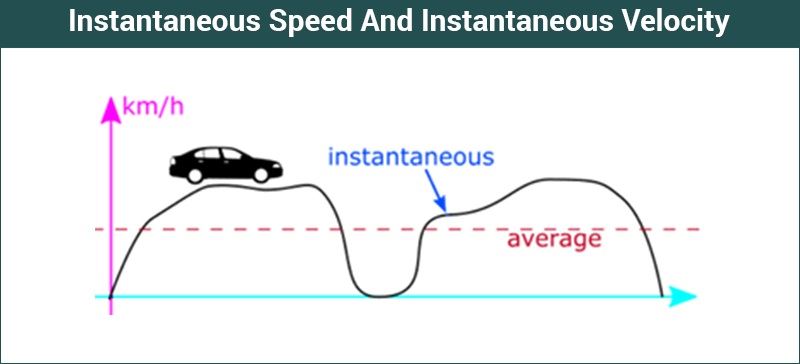
So, in this figure, we find that we’ve plotted position or distance at an instant on the Y-axis. ( Distance at an instant = t -> 0) Therefore, we have time on the x-axis. The curve, therefore, represents the total velocity. Now, you need to draw a tangent on the curve. It must cut the point at which you want to find out the instantaneous velocity. Now, draw a perpendicular from that point on the time axis. Therefore, you will find a particular point of time, say t0. Now, draw the tangent to the y-axis too. Check out where it cuts, and note down the point, say x0. Now you need to find the slope of this tangent line to get the value. So, you simply need to divide x0 by t0 and you will get velocity or v at t0. This, therefore, is your final value.
Average velocity graph
Moreover, you can also find the average velocity from this graph. So, consider a portion of the curve of which you want to get the average velocity. So, again you need to draw a line that cuts that part of the curve. Therefore, you get two points on the curve. Draw two lines from there on both the x axes as well as the y axes. Therefore, you have found two points on the time axis. Moreover, corresponding to these two points, you have also found two points on the position axes. So, now find the difference between the two points on both axes. After this, divide the distance by the change in time. Therefore, you get the ratio of change in distance to the time interval that you have considered. So, this is your average velocity in a particular time interval.

Instantaneous velocity calculator
One thing you must remember is that instantaneous velocity can be positive, negative, or zero. So, obviously, you can guess if the body is at rest, then the instantaneous velocity will be zero. This is because the change in distance is zero. Positive instantaneous velocity is what we have been discussing mostly till now. However, consider a case when an object in motion has already reached a point. So now, it is returning to its point of origin by retracing the same path. Therefore, in this case, the direction of the vector will be negative. So, instantaneous velocity will be negative. Therefore, when you are using the value of instantaneous velocity, make sure you are using the proper sign. Your entire calculation can go wrong if you make a mistake with the sign or simply do not give it. Hence, a small mistake can give weird resultant values.
However, there is another instance when instantaneous velocity can be 0. Suppose the object moves in a circular path. So, when the object has reached its starting point, the neat displacement becomes zero. Therefore, the position is zero itself, and so instantaneous velocity is again 0.
The SI unit of instantaneous velocity is the same as that of velocity. So, it is m/s. So, make sure when you are calculating it, you give the unit as per the units of the other two. Therefore, the resultant unit might be km/hour or km/min or anything else. It totally depends on the combination. Moreover, generally, if you need the value of the instantaneous velocity for bigger calculations, you need to convert them. So, either convert the units individually. Or, on the other hand, after you get the value, you can convert it as a unit of velocity.
Instantaneous velocity example
So, for example, you have the following function of time-
x = 3t + 4t^2
You have to find the average velocity when the time t is at 2 seconds.
So, let us solve it.
To find the instantaneous velocity, we will first differentiate the function.
So, dx/dt = d/dt (3t) + d/dt (4t^2)
Now, dx/dt as we know is the instantaneous velocity at t seconds.
Therefore, v (t) = 3 + 8t
So, now we will replace ‘t’ with 2 seconds.
Therefore, velocity at 2 seconds, v(2) = 3 + (8 x 2) = 19
So, it will be 19 m/s, but as a vector.
Instantaneous velocity FAQs
Does instantaneous velocity have a direction?
Yes, just like normal velocity, instantaneous velocity too has a direction. It is so as it considers the displacement of a body in motion at that time. Therefore, the distance it covers does not matter. So, this is what makes it different from instantaneous speed.
Can instantaneous velocity of an object be the same as that of the average velocity?
Yes. It can be exactly the same as the value of the average velocity of a body in motion. It can also be lesser or greater than that,
Is instantaneous velocity a vector?
Yes, instantaneous velocity is a vector.
Can instantaneous velocity be negative?
Yes, instantaneous velocity can be negative.

Is instantaneous speed a scalar quantity?
Yes, instantaneous speed is a scalar quantity.
Is instantaneous velocity the same as that of acceleration?
No, they are completely different entities. Instantaneous velocity is the velocity of a body in motion at a particular point in time. Acceleration is the rate of change of velocity of a moving body. Hence, its SI unit is m/s^2. Both of them, therefore, measure very different things. If the velocity is constant, acceleration will be zero for the moving body.